Όπως είδαμε στο προηγούμενο μάθημα, για να μετρήσουμε το εμβαδόν οποιουδήποτε σχήματος και κατ’ επέκταση οποιασδήποτε έκτασης, πρέπει με διαφόρους τρόπους να το μετατρέψουμε στο γνωστό γινόμενο β · υ, δηλαδή σε δύο μετρήσεις μήκους ευθυγράμμων τμημάτων. Και κατόπιν, αφού το λογαριάσουμε, μπορούμε να το εκφράσουμε και ως προς ένα τετράγωνο με πλευρά 1 μ., δηλαδή 1 τετραγωνικό μέτρο, ή σε κάποια από τις υποδιαιρέσεις του.
(παρακολουθήστε την εικόνα προσεχτικά)

Γιατί όμως προτιμάμε το τετράγωνο και όχι τον κύκλο;
Έχουμε κατορθώσει να τετραγωνίσουμε άραγε και τον κύκλο;
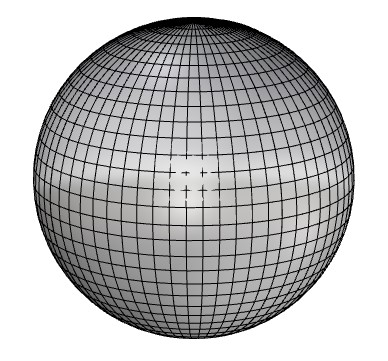
Η πραγματικότητα είναι πως προτιμούμε τα τετράγωνα, διότι αν κάναμε το παραπάνω με κύκλους, όπως φαίνεται παρακάτω, παρατηρούμε ότι μεταξύ των κύκλων υπάρχουν κενά τα οποία δεν μπορούν να υπολογιστούν, όσο κι αν προσπαθούμε με εργαλείο το σχήμα του κύκλου. Πάντα θα μένουν περιοχές εκτός.
(παρακολουθήστε την εικόνα προσεχτικά)

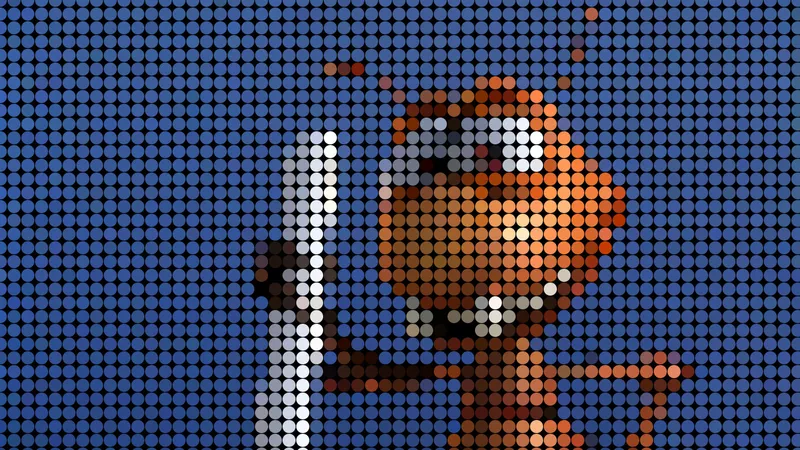
Άρα τελικά, μας συμφέρει περισσότερο ακόμη και μια σφαιρική επιφάνεια να την προσεγγίσουμε με το σχήμα του τετραγώνου παρά με αυτό του κύκλου. Στην πραγματικότητα, ακόμη και ο παραπάνω κύκλος που βλέπουμε δεν αποτελείται από μία καμπύλη γραμμή αλλά από πολλές μικρές τεθλασμένες. Οι οθόνες που βλέπουμε αυτή τη στιγμή αποτελούνται από pixels = κουκίδες, οπότε την καμπύλη την αποδίδουν με ευθύγραμμα τμήματα.


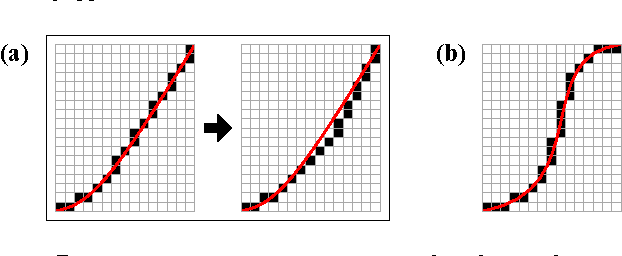
Πώς εξηγείται όμως αυτό;
Γιατί μπορούμε να καταλάβουμε στην παρακάτω εικόνα ότι είναι ένα αιλουροειδές, αν και είναι φτιαγμένη με τετράγωνα και όχι με καμπύλες;
Αυτό δεν αποτελεί φαινόμενο με το οποίο ασχολείται η φυσική, αλλά η βιολογία, διότι έχει να κάνει με την κατασκευή του οφθαλμού του ανθρώπου και του τρόπου που ο εγκέφαλος επεξεργάζεται τις πληροφορίες που δέχεται από το περιβάλλον του. Αυτό μάς επαναφέρει, όπως όλα, στην δημιουργία του ανθρώπου υπό του Θεού και στο ότι Εκείνος είναι τα έχει ορίσει να λειτουργούν έτσι. Αν ήθελε ο Θεός, θα λειτουργούσαν τελείως διαφορετικά οι κανόνες και οι νόμοι της φύσης και ο κύκλος θα μας βόλευε πιο πολύ από το τετράγωνο.
