Για να μετρήσουμε το εμβάδον εμείς οι άνθρωποι ουσιαστικά κατασκευάζουμε σχήματα και τρόπους που δεν υπάρχουν πουθενά στη φύση. Αν σας πω να μου μετρήσετε το εμβαδόν της παρακάτω πλαγιάς, θα δυσκολευτείτε πολύ να το κάνετε, και θα δυσκολευτείτε επίσης ακόμη και να ορίσετε μια περίμετρο σ’ ένα συγκεκριμένο οικόπεδο, διότι μετράμε σε ευθείες και όχι γενικά σε σχήματα, που σημαίνει ότι πρέπει να μπορέσουμε να κινηθούμε σε ευθεία ή με κάποιο τρόπο να μετρήσουμε με ευθύ τροπο.

Η αλήθεια είναι ότι εμείς οι άνθρωποι κατασκευάσαμε εκ του μηδενός τα σχήματα που μας βολεύουν να υπολογίζουμε και να μετράμε (τετράγωνο, τρίγωνο, ορθογώνιο κτλ) και κατόπιν υπολογίζουμε τα εμβαδά των επιφανειών τεμαχίζοντάς τες σε σχήματα που μπορούμε να μετρήσουμε τις πλευρές τους και να υπολογίσουμε το εμβαδόν τους.
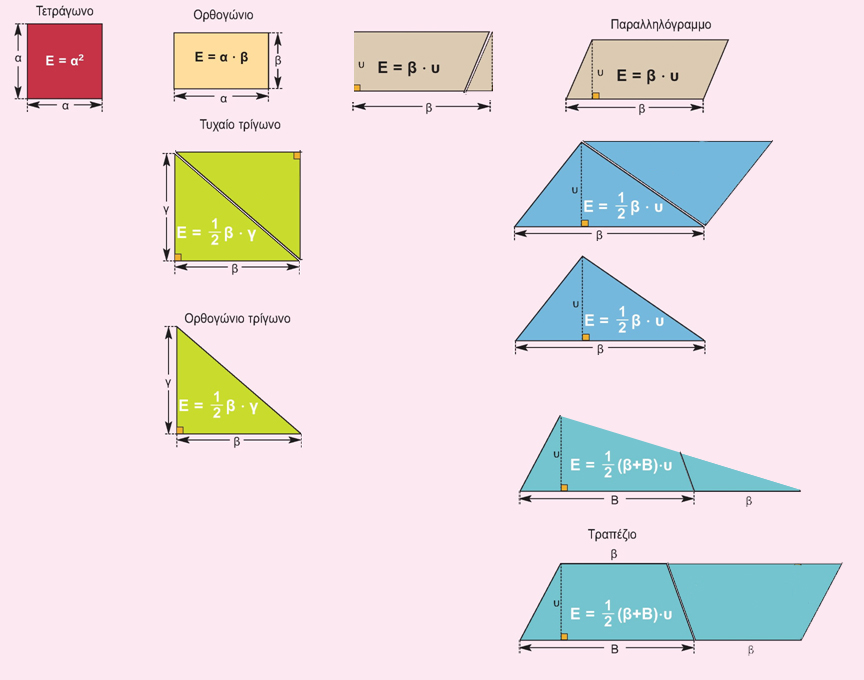
Τα πιο διαδεδομένα σχήματα των οποίων το εμβαδόν μπορούμε εύκολα να υπολογίσουμε εφόσον μπορούμε να μετρήσουμε τα ευθύγραμμα τμήματα που μας χρειάζονται φαίνονται στο παρακάτω παιχνίδι και τα μαθαίνουμε ήδη από το Δημοτικό:
Ωστόσο, αυτό που πολλές φορές ξεχνούν οι δάσκαλοι να μας πουν είναι ότι τελικά όλα τα παραπάνω σχήματα τα υπολογίζουμε με τον ίδιο τύπο β · υ. Φαίνεται παράδοξο γιατί βλέπουμε διαφορετικούς τύπους, αλλά στην πραγματικότητα, όλα τα σχήματα για να τα υπολογίσουμε τα κάνουμε ορθογώνια και στο τέλος τετράγωνα, που είναι μια ειδική περίπτωση ορθογωνίου, η οποία μας βολεύει στις μετρήσεις του εμβαδού, του οποίου η μονάδα μέτρησης είναι το τετραγωνικό μέτρο, διότι για τον υπολογισμό του απαιτούνται οι ελάχιστες δυνατές μετρήσεις, δηλαδή το μήκος μίας πλευράς του.