Παίρνοντας τη σκυτάλη από το εμβαδόν, όπου τελικά όλα τα κάναμε και τα βλέπαμε τετράγωνα, στο φυσικό μέγεθος του όγκου, όλα τα κάνουμε κύβους που είναι ουσιαστικά η χωρική έκφραση του τετραγώνου. Το τετράγωνο υπάρχει στον δισδιάστατο χώρο, σε επιφάνειες, ενώ ο κύβος έχει τρεις διαστάσεις και ανήκει στον χώρο και δημιουργείται προεκτείνοντας στην τρίτη διάσταση, ίση με τις άλλες δυο διαστάσεις του τετραγώνου. Ή αλλιώς, θα λέγαμε ότι βάζουμε τόσα τετράγωνα το ένα πάνω στο άλλο, ώστε το ύψος τους να είναι ίσο με των άλλων δύο διαστάσεων.
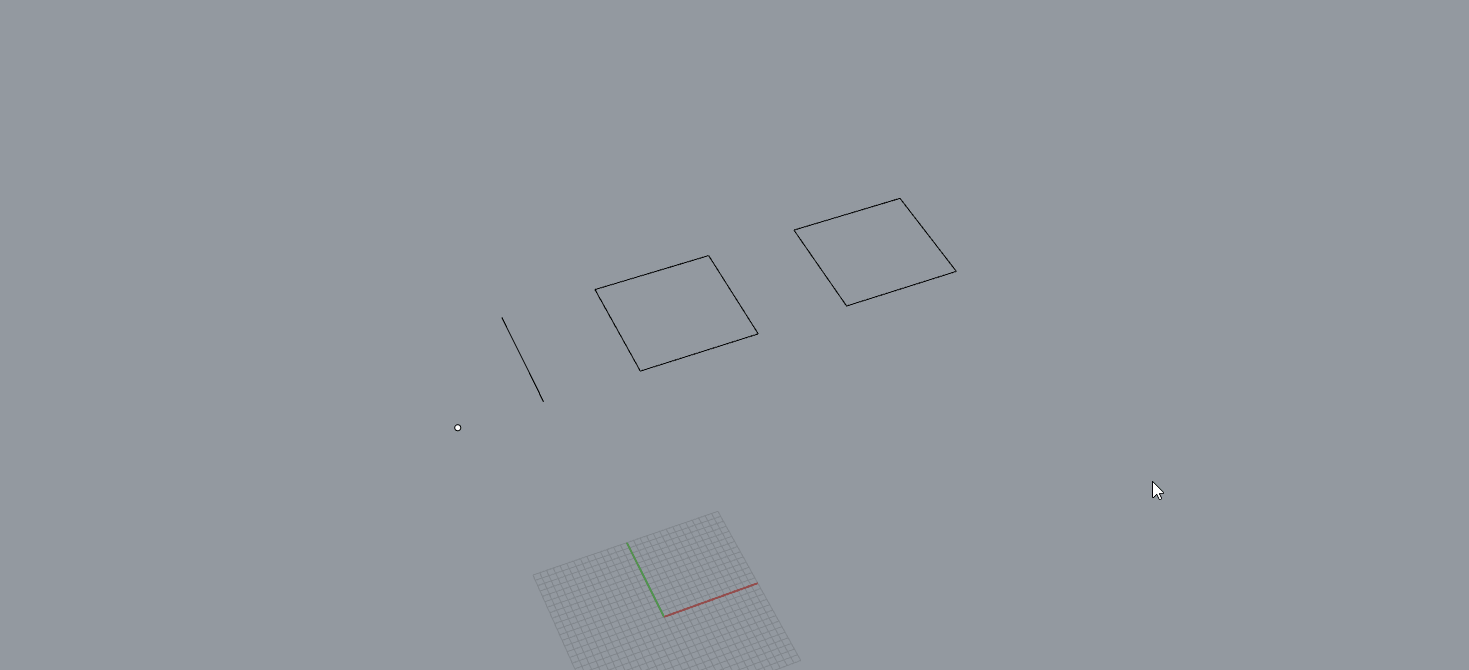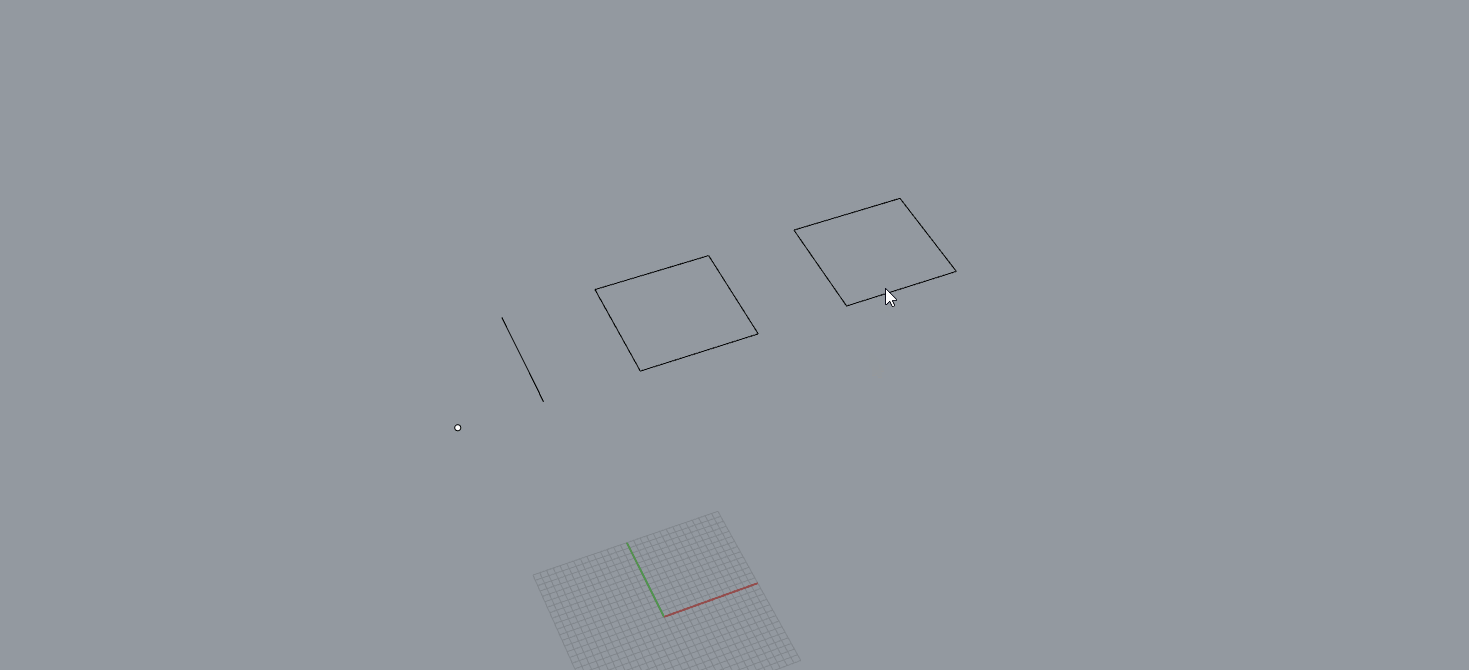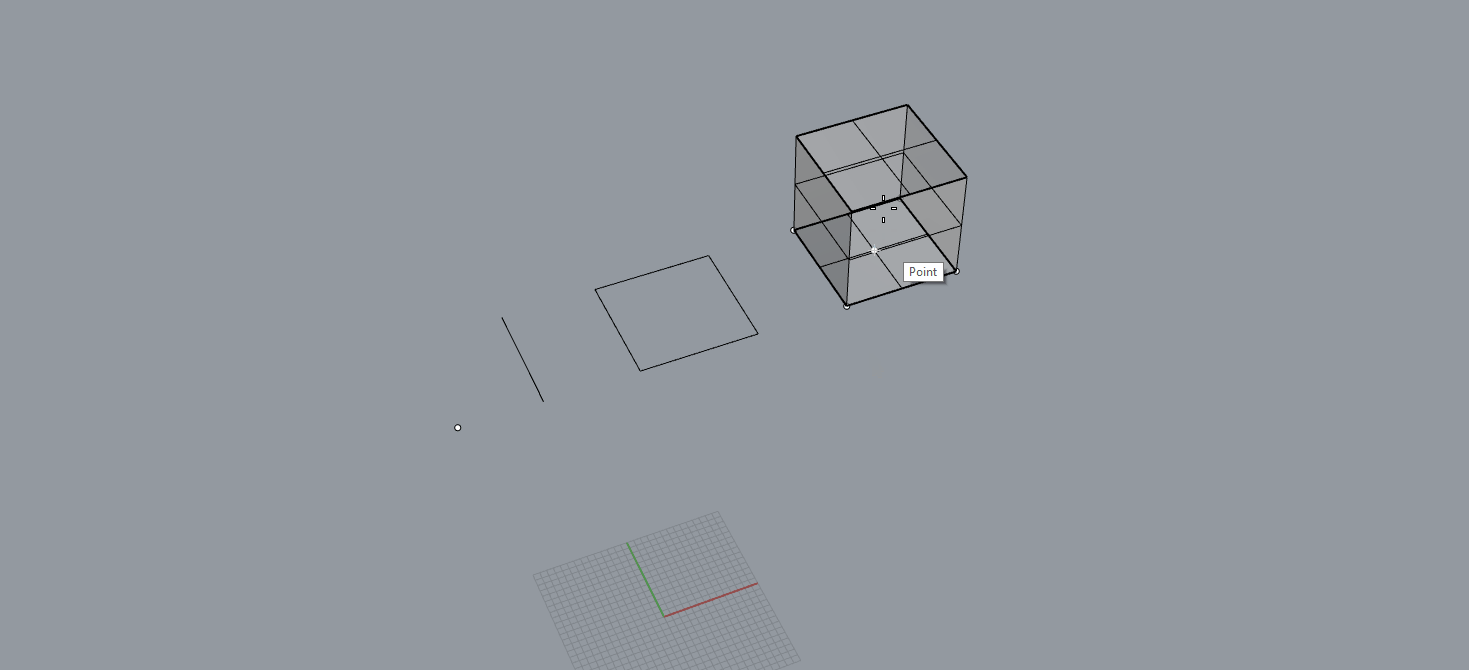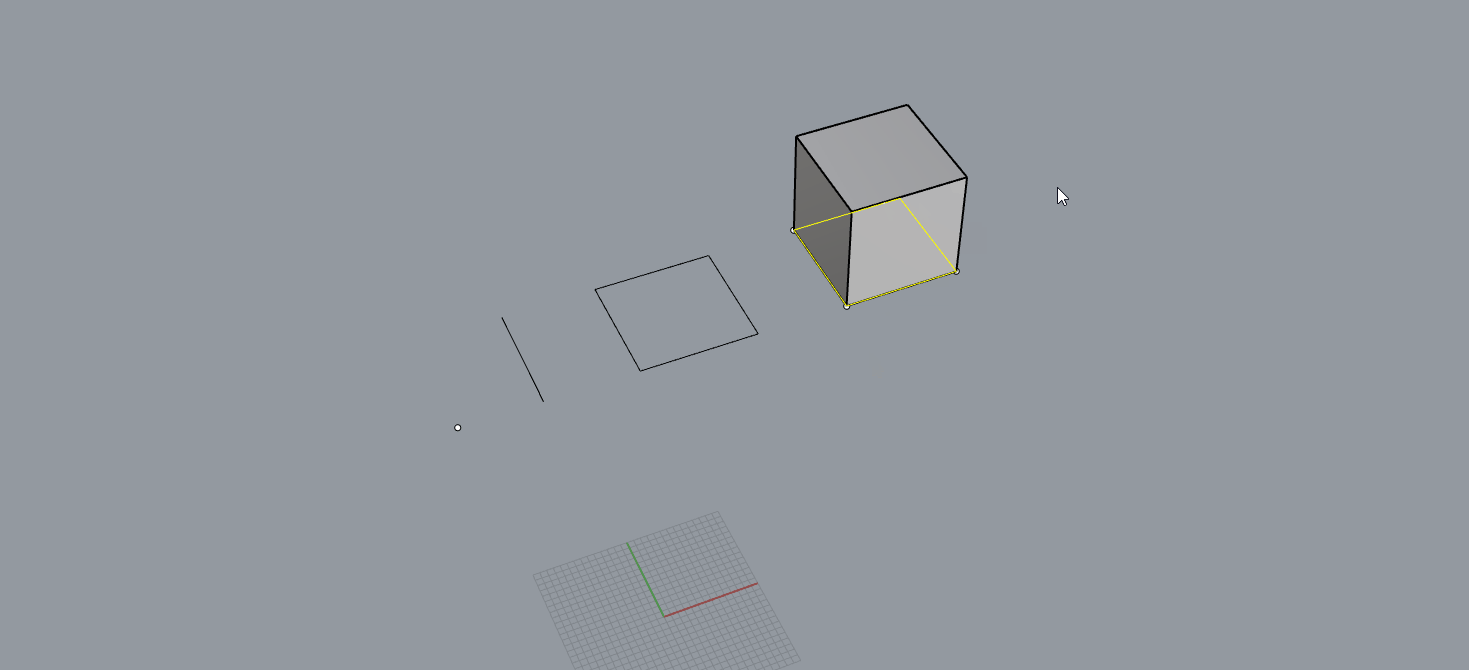

Αυτό σημαίνει ότι χρειαζόμαστε τρεις διαστάσεις για να υπολογίσουμε τον κύβο, μ(ήκος) • π(λάτος) • ύ(ψος). Όμως, πόσο εύκολη είναι η χρήση αυτής της φόρμουλας;
Στην πραγματικότητα, δεν είναι καθόλου εύκολη, διότι τα περισσότερα αντικείμενα δεν έχουν όγκο κανονικών στερεών όπως είναι τα παρακάτω (π.χ. κύβος, πυραμίδα, κύλινδρος).
Τα περισσότερα αντικείμενα ή στερεά, έχουν ακανόνιστο σχήμα όπως είδαμε και στο προηγούμενο μάθημα με το τραπέζι. Και μάλιστα, μπορούν πολλές φορές να αλλάζουν και σχήμα, υπό προϋποθέσεις. Αν θέλουμε να είμαστε καθόλα ακριβείς, όλα τα σώματα μπορούν να αλλάξουν σχήμα, αλλά κατά την αλλαγή του σχήματος ως επί το πλείστον χάνουν ορισμένες ή και όλες τις ιδιότητες που είχαν. Για παράδειγμα, όταν λιώνουμε ένα μεταλλικό αντικείμενο, το παραγόμενο αποτέλεσμα παραμένει μεταλλικό (όταν ψυχθεί ξανά), αλλά δεν έχει την αρχική μορφή και ούτε τις αρχικές ιδιότητες του προηγούμενου σχήματος (χωρητικότητα, σταθερότητα, μεταβλητότητα κτλ).


Άρα τελικά, πώς μας συμφέρει να μετράμε τον όγκο ενός στερεού, όταν τα περισσότερα έχουν ακανόνιστα σχήματα, στα οποία οι ευθύγραμμες μετρήσεις μήκους που έχουμε μάθει να κάνουμε, δεν μας βοηθάνε;
Όπως ακούσαμε και στο βίντεο, χρησιμοποιούμε έναν τρόπο άλλον, όπου με τη βοήθεια του νερού και ενός ογκομετρικού δοχείου, είτε αυτό είναι ογκομετρικός κύλινδρος, είτε μια δεξαμενή γνωστού όγκου (ορθογώνιο παραλληλεπίπεδο, του οποίου γνωρίζουμε εκ κατασκευής τον όγκο και το έχουμε βαθμονομήσει), μετρούμε δια της αφαιρέσεως τον όγκο του στερεού.
Είχαμε πει στο προηγούμενο μάθημα ότι ο όγκος ενός στερεού μάς δείχνει τον χώρο που καταλαμβάνει ένα στερεό σώμα και που δεν μπορεί άλλο στερεό σώμα να καταλάβει, ειδικά μεγαλύτερο από πρώτο. Στην από πάνω περίπτωση βλέπουμε ότι τοποθετώντας το σώμα εντός του κυλίνδρου το νερό ανεβαίνει, γιατί το νερό πλέον δεν μπορεί να καταλάβει τον χώρο όπου βρίσκεται το στερεό. Αντιστοίχως και στο από κάτω βίντεο, βλέπουμε ότι όταν μπει το σώμα μέσα στη γεμάτη κούπα νερό, ποσότητα του νερού χύνεται εκτός της κούπας γιατί δεν μπορεί πλέον να καταλάβει τον χώρο αυτόν, του στερεού σώματος.
Αλλά πώς μετράμε τον όγκο πολύ μεγάλων αντικείμενων όπως π.χ. βουνά κτλ;
Κατασκευάζουμε άραγε τεράστιους ογκομετρικούς σωλήνες;
Η απάντηση είναι όχι. Στην πραγματικότητα μπορούμε απλώς να προσεγγίσουμε τον όγκο τους κατασκευάζοντας υπό κλίμακα μοντέλα τους, και κάνοντας υπολογισμούς. Πλέον, με τα υπολογιστικά συστήματα που έχουμε, όλα αυτά γίνονται αυτόματα και βγαίνει η ογκομετρική τιμή χωρίς να καταλαβαίνει κάποιος πόσο πολύπλοκοι υπολογισμοί γίνονται από πίσω.